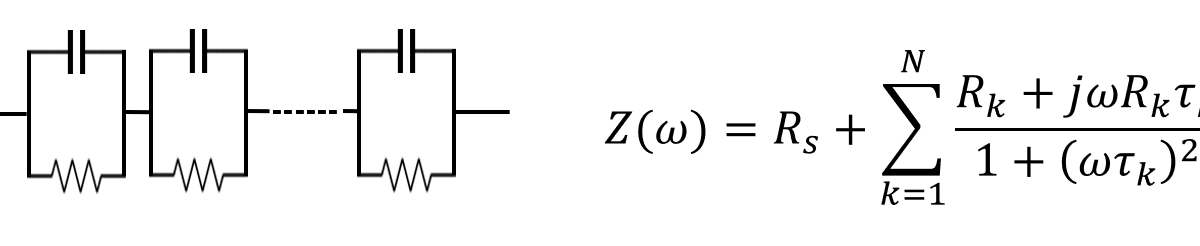Using a series of Voigt elements(resistance and capacitance in parallel) to model the EIS data of any type is a recurring theme. Effectively, the method is to fit the data with the above circuit diagram or equivalently, the equation on the right.

In the equation, j represents the imaginary number(√-1), τ is the time constant(i.e. RxC) for each Voigt element. The ways to calculate/choose the various time constants and resistances differ, but it is widely accepted that a combination of “relaxation times” or Voigt elements will explain any impedance spectrum.

This post will summarize a number of different approaches that employ this combination and will attempt to discuss advantages and disadvantages of some of them that we had experience with. Initially, these were used for checking with compatibility with the Kramers-Kronig relations (i.e. stability, linearity and causality). Currently, they are further used as ways to interpret data to achieve certain results.

Measurement Model approach from Aggarwal and Orazem: This is based on a series of papers from Aggarwal and Orazem that can be found here, here and here. In this approach, the number of Voigt elements and which side of the data(real or imag) will be fit are selectable. Once the fit is done, the counterpart is calculated and compared. An implementation of this is freely available here from the Orazem group for download on ECSArxiv here. The software further yields statistical analysis of the results and has the option of using a custom weight array if the error structure is known. Though the software requires some experience to master, the vast information makes the effort thoroughly worth it.

Boukamp Approach: In the Boukamp approach based on a publication from B. A. Boukamp here, a system of linear equations are solved. The time constants(RxC) are chosen from the spectrum under question and fixed throughout. Then, either the real or the imaginary part is used to calculated the resistance values for the said time constants. Afterward, the counterpart of the data is calculated with the calculated R values. The process of resistance calculation is a linear fit, therefore it does not require any initials. The only user input is how the time constants are going to be selected. The commercial Gamry software uses this approach for checking compatibility with the Kramers-Kronig relations. I have been using this as a former Gamry employee and a current Gamry user for a while now. Recently, I wanted to dig deeper to see what the R values were doing.

Here is an implementation from me that allowed me to investigate the approach in more detail. The Python code requires Numpy and Matplotlib. It was surprising to see how oscillatory and high the R values calculated come out. Since the time constants are picked evenly throughout the frequency range, it is very possible that they do not overlap with the true time constants. Ultimately, the math works and the data does get fit as long as the number of time constants used are large enough. The method is very appropriate for a user friendly software package, as it simplifies the UI greatly. The user just clicks go and the software takes care of the rest really quickly as the math is linear.

Distribution of Relaxation Times(DRT): More recently, a more continous and generalized version of the above approaches called DRT is employed. There are way too many papers to credit that employ the method in various ways but one that I really like is by Tuncer and Macdonald here. Ultimately, this approach attempts to calculate the appropriate amplitudes for all the time constants that fit the data to the best precision. A couple of free software packages that achieves this are available by the group of F. Ciucci in their github page(here).

In our experience, DRT effectively transforms the spectrum from a frequency domain to a time constant domain. This is useful in the understanding and the visualization of the results. It might aid in the attempt to gather fundamental information about the electrochemical processes in the system under test.

To summarize, any properly linear and stable electrochemical impedance spectrum can be expressed as a sum of individual resistance capacitance combintations. The details of how this is achieved change the specifics, however, ultimately all methods are advantageous in their own way. None of these on the hand, relieve the experimenter of the duty of interpreting and making the connection of the data with the fundamental electrochemical processes.